Let’s start with a comparison between two qubits: q0 and q1. They can hold 4 possible value:
- q0 = 0, q1 = 0
- q0 = 0, q1 = 1
- q0 = 1, q1 = 0
- q0 = 1, q1 = 1
An equality check should return 1 if we are handling cases number 1 or 4, and return 0 if we are handling cases 2 or 3.
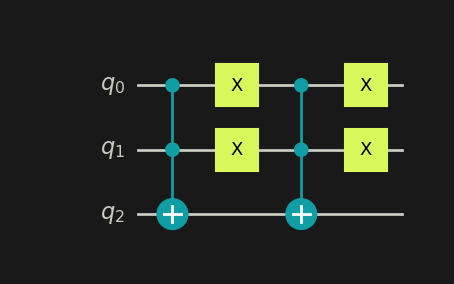
One approach to creating the circuit would be to directly check if they are both 1 or are both 0. Checking if they are both 1 is using a Toffoli gate between them. Checking if they are both 0 is done by applying X gates to both q0 and q1, followed by a Toffoli gate, and ending with X gates on q0 and q1 again to return them to their original state. After we check it we can perform an “AND” logical operation between these results, which is yet another Toffoli gate, and than we get our answer!
Can we improve it? Of course!
To do that, we should note that cases 1 and 4 are inherently different - q0 and q1 can’t be both 0’s and 1’s simultaneously (superposition does not bother us since, intuitively, the algorithm is applied to each state separately). Therefore, we can use both of the checks on the same result qubit. If one of the cases is correct, the result will be 1, and otherwise, it will be 0. We just saved two auxiliary qubits and an expensive Toffoli gate!
The algorithm can be shown in the attached image.