KAKURO - A CONSTRAINT SATISFACTION PROBLEM
Background:
Kakuro is a logic puzzle, often referred to as a mathematical transliteration of the crossword. The puzzle is played on a grid of filled and empty cells. The filled cells contain the required sum for the matching empty cells. The objective of the puzzle is to fill the empty spaces under two constraints:
- Two cells on the same row/column cannot have the same number.
- The sum of the cells on each row/column should equal the matching filled cell.
Problem:
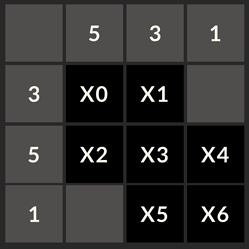
The challenge for the Classiq Coding Competition was to solve the following Kakuro puzzle using Grover’s Search Algorithm, with these specific constraints.
Winning Metric:
The winners were chosen based on the lowest number of CX gates in their oracles.
We verified the submitted CX gate count and executed the full circuit to confirm the correct solution was found.
FIRST PLACE - Adam Glos and Özlem Salehi, Poland
Taking advantage of the constraints’ relationship to one another, this team prepared a state that removed 5 of the 11 constraints from the oracle!
For the remaining constraints, Adam and Özlem optimized for CX gate count by using in-place arithmetic, wise orderings of constraints, and relative phase Toffoli (RCCX) gates. They successfully created a Grover’s Search circuit with only 86 CX gates in their oracle.
For a Jupyter Notebook of the first place oracle and Grover Search, see here.
Read their full explanation here.
SECOND PLACE - Naman Jain, India
Splitting the constraints into their 5 different types - single-qubit register inequality, multi-qubit register inequality, addition of constant, sum of quantum registers, and qubit register equality - Naman optimized for CX gate count in the implementation of each constraint.
For the phase kickback, he opted for more qubits and less depth with a series of CCX gates vs an expensive, multi-controlled Toffoli gate. After reordering the constraint implementations, using the Margolus gate, and checking qubit register equality directly, Naman successfully created a Grover’s Search circuit with only 126 CX gates in his oracle.
For a Jupyter Notebook of the second place oracle and Grover Search, see here.
Read his full explanation here.
THIRD PLACE - Team Tinubu: Thomas Frossard, Ayoub El Qadi, Quoc Viet Nguyen, Marcelin Gallezot, France
Splitting the constraints into their 3 different types - single-qubit register (in)equality, multi-qubit register (in)equality, and summations - Team Tinubu optimized for CX gate count in the implementation of each constraint.
They reduced CX gate count by trading off a larger qubit count for a shallower depth with relative phase Toffolis, storing only the necessary information resulting from each constraint implementation, and optimizing qubit reuse. Team Tinubu successfully created a Grover’s Search circuit with only 134 CX gates in their oracle.
For a Jupyter Notebook of the third place oracle and Grover Search, see here.
Read their full explanation here.