Measuring Depth and 2-Qubit Gate Count

General
1

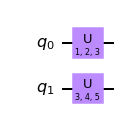
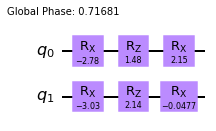
Here’s a guide to measuring the depth and 2-qubit gate count for your QASM submissions.

Step 1: Import QASM code into Qiskit

If not previously installed, install Qiskit.

Import QASM as a string or file.

String:

from qiskit import QuantumCircuit

# Paste QASM contents between three sets of quotes
qasm_str = 
"""OPENQASM 2.0;
   include "qelib1.inc";
   qreg q[2];
   creg c[2];
   h q[0];
   cx q[0],q[1];
   measure q -> c;"""

qc = QuantumCircuit.from_qasm_str(qasm_str)

File:

from qiskit import QuantumCircuit

qc = QuantumCircuit.from_qasm_file("/path/to/file.qasm")

Step 2: (OPTIONAL) Decompose Circuit to Basis Gates As Needed

Decompose any functional blocks or multi-qubit gates into single- and two-qubit basis gates.

qc = qc.decompose()
qc = qc.decompose()
# repeat as needed, checking with draw() to see circuit status
qc.draw()

Repeat as needed until circuit fully decomposed.

Step 3: Measure Depth and 2-Qubit Gates

print(qc.depth())
print(qc.count_ops())

For the following result, submit a depth of 153 and a two-qubit gate count of 130.

153
OrderedDict([('cx', 130), ('u1', 112), ('u2', 32), ('u', 10), ('measure', 9)])

For a full example, see here.

1 Like
2

You can also do:

qc = qc.decompose().decompose()

Instead of adding lines, as needed, just add .decompose() as needed.

3 Likes
3

The following should also work for decomposing the circuit

from qiskit import transpile
qc = transpile(qc, basis_gates=['u', 'cx'])
4 Likes
4

Oh, I found this topic too late!

I was almost sure that the depth of the circuit refers to the depth wrt CX gates, ignoring 1q gates. In my experience, this is the most common setting when one talks about circuits consisting of CX gates and arbitrary 1q gates.

Is there a rationale for including all gates into account, and not just CX gates?

And a follow-up question. Is it correct that this circuit will be considered to have depth 1
image
while this circuit will be counted as having depth 3
image
?

(the circuits are related by an Euler decomposition). In other words, is it correct that the most general single-qubit gate is counted as a single gate?

5

Yes, I believe the most general single-qubit gate is counted as a single gate. But the best way for you to test it is to follow the steps above in the thread, e.g. use the decompose() function